查询优化

1.引言

当我们学习SQL时，我们提供了一个有用的模型来解释查询是如何被执行的。首先，我们通过From子句得到了所有的行，然后我们通过Where子句过滤掉那些不需要的行，然后等等。这种模型可以保证我们能得到正确的查询结果，但它并不是数据库实际执行的过程。数据库可以改变这些操作的顺序来达到更好的性能。在这门课（CS186）中，我们通过I/O的次数来衡量一个操作的性能。查询优化主要关注的便是找到最小化需要I/O次数的查询计划。查询计划是指能够得到正确查询结果的操作序列，我们会用关系代数来表达它。例如以下的SQL语句:

SELECT name,time FROM Sailors INNER JOIN Reserves 
ON Saliors.bid=Reserves.bid WHERE bid = 3

它的一个查询计划如下：

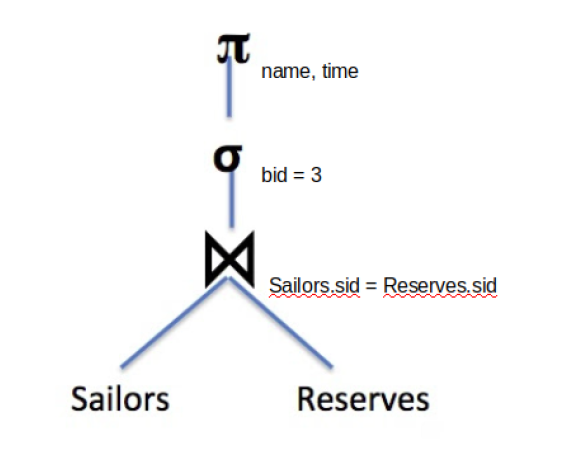
首先将两个表进行连接（⋈），然后进行过滤（σ），最后投影（Π）出所需要的列，这样这个查询计划就能够得到正确的结果了！但它可以优化吗？

2.选择性估计

查询优化有一个难点，就是在我们执行一个查询计划之前，我们是无法具体知道它在I/O上的消耗次数。它会带来两个重要影响：第一是我们不可能每次都能找到最优的查询计划，只能通过启发式方法和量化方法寻找较优解；第二是我们需要用一些手段来量化查询计划的查询代价。有一种名为选择性估计的方法能帮助我们衡量一个查询计划的代价。

（前置知识：数据库里的“一行”被称为记录，有时也被称为元组。所有记录以页为单位在磁盘上组织。详见第2讲。）

我们认为一个操作的选择性是指有多少百分比的数据页在通过它后能够到达下一步。这种衡量手段十分有用，因为我们可以把Where这种能够过滤掉多数数据的操作移到查询计划前期，从而大幅减小后面步骤中所要处理的数据数量。

大部分的选择性估计的公式其实很直白，它是基于概率论的计算方式。例如X有1，2，3三个取值，我们认为数据表中的X是等概率分布的。那么对于条件Where X=3这个过滤操作，我们便可以算出它的选择性是1/3，即只有1/3的记录能够通过它到达下一个操作。以下列出了若干个选择条件的选择性估计值：

• X=a： 1/(X的所有取值数)
• X=Y： 1/max(X的所有取值数，Y的所有取值数)
• X>a： (max(X)-a)/(max(X)-min(x)+1)
• A AND B： A的选择性*B的选择性

此处a是常量，X、Y是变量，A和B各是独立的选择条件。这里仅是对于整数的选择公式，对于浮点数还有另外的公式。

3.连接子句的选择性

对于A和B两个表连接的时候，假如没有任何的筛选，那么就会有|A|*|B|（|A|表示表A的行数）个元组，因为两个表中的元组会两两结合。而我们一般会有自然连接条件，即A.xxx=B.xxx，根据上面的公式，这个连接条件的选择性S=1/max(X的所有取值数，Y的所有取值数)。我们便可以估算这次选择后会产生多少行数据： \(\frac{|A|*|B|}{S}\)

4.常用的启发性方法

实际业务中常常会有复杂的查询，这些查询有过多对应的查询计划而难以分析。但它们有相当一部分是低效的。我们需要一些方法来缩减真正有必要分析的查询计划。我们总结出了一些剪枝的方法：

1. 将投影（Π）操作和选择（σ）操作尽可能提前（注意此处的选择是Where而不是Select）
2. 使用左深树的查询结构（left deep plan）
3. 尽可能晚使用连接操作

第一种剪枝方法就是指将各种缩减数据量的操作进行提前。将选择操作提前的好处不言而喻：它减小了后面的操作所要处理的数据量。而为什么说提前投影操作也是有用的呢？因为投影操作减小了每一条记录的大小，意味着我们能在一条数据页中存放更多的记录，从而减小所需要的数据页数量。当然我们提前投影操作时，要考虑到后面的查询的需要。例如后面的查询中有SELECT或WHERE子句需要某一列的数据，我们就不能提前用投影操作把这一列给去掉。

第二种剪枝方法是左深结构。它是说每个连接节点的右子节点都是一个原始的表，而不能是连接而成的中间结果。以下是一个左深结构的例子：

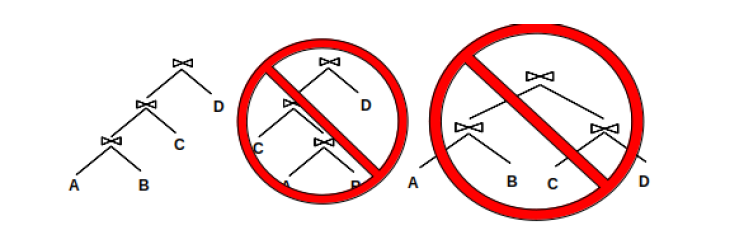
A、B、C、D是原始的表，它们只能在叶子节点上，且除了起始的连接所需要的表外，都处在连接节点的右子节点。总结以下顺序就是：A和B连接，连接结果再和C连接，再将连接结果和D连接。

这种结构有两个好处。第一是它大大减小了查询计划所占用的空间。尽管整个计划所占用的空间仍然很大，但这样可以将它划分为较小的若干个计划。另外，这些计划可以管道化，我们可以直接将前一次操作的结果用于下一次操作，而不用将这个中间的连接结果写入磁盘，从而大大减小磁盘I/O数。

第三种剪枝操作也很容易理解，连接操作会产生大量的数据页，令在其之后的操作需要处理更多的数据。

5. System R的第一轮操作

在这门课（CS186）中我们需要学习的查询优化器称为System R。它使用了上面提到的所有的启发性（剪枝）方法。System R的第一步是决定如何更佳或更令人关注地从表中获取数据（“令人关注的”会在后面论述）。

我们在第一轮时从一个表中获取数据有两种选择：

1. 全表扫描
2. 使用索引扫描（通过表中建立的每一个索引，本课使用B+树索引）

对任意一种扫描方法，我们都只返回满足和表对应的选择条件的记录（使用第一种剪枝方法）。因为我们这里还只是考虑从每个表分别获取数据，所以对于某几列数据来自于多个表（连接）的场合还不使用这种方法。这意味着不管我们采用哪种扫描方法，选择条件的选择性都是相同的。

但是它们所需要的I/O数量却是不一样的。对于表P，一次全表扫描需要[P]（[P]表示表P所占据的数据页数）次I/O，因为它需要读每一个页。

（B+树索引有三种实现方案，第一种是叶节点本身便存放数据，第二种是叶节点存放若干条键值对，键是索引所使用的属性，值是指向数据页中实际记录的指针，第三种和第二种类似，但它将相同键的键值对合并，使用一个指针数组来存储每一条指向的实际记录。）

对于索引扫描，所需要的I/O数量依赖于表中的记录是如何存储的以及索引是否是聚集索引。对于第一种索引实现，扫描的I/O消耗为：到达叶节点上面一层的消耗+读取的叶子数。

我们并不一定要读每一个叶节点，因为我们可以对索引所使用的列使用选择条件实现筛选。这是因为数据是在叶节点里按顺序存储的，所以可以直接到达所需要的起始叶节点，并且可以一路前进直到选择条件不在为真。

例：提供以下信息：

• 表A有[A]数据页
• 对C1属性有一个索引，使用第一种实现，且高度为2
• 有两个查询条件：C1>5 and C2<6
• C1和C2的值都在1-10的范围内

我们可以算出选择性为0.25，因为两个选择条件的选择性都是0.5，乘起来便是0.25。但我们不能用C2条件来减小所搜索的数据页的数量，因为索引是建立在C1之上的。我们可以用C1条件进行选择，这意味着我们只需要看0.5[A]个叶节点就行了。但我们也需要读取2个索引页来判断从哪个叶节点开始。因此所需要的I/O数为2+0.5[A]。

对于后两种实现方案，公式会有所不同。扫描的消耗为：

到达叶子节点上面一层的消耗+读取的叶节点数+读取的数据页数

后两项我们可以使用选择性（建立在索引上的选择条件）进行缩减。对于聚集索引，所需要读取的数据页数是总数据页数乘以选择性。但对于非聚集索引，因为要对每一条记录进行I/O，所以读取的页数是选择性乘以总记录数。

（聚集索引是指数据的物理存储顺序与索引顺序相同，意味着同一叶节点的索引对于的记录能存放在同一数据页中；非聚集索引则没有这个相同顺序，意味着一个叶节点内的索引能分别指向不同的数据页。）

例：提供以下信息：

• 表B有[B]数据页
• 对C1属性有一个索引，使用第二种实现，且高度为2，有[L]个叶节点页
• 有两个查询条件：C1>5 and C2<6
• C1和C2的值都在1-10的范围内

第一轮操作的最后一步是决定将哪些访问表的计划推进到接下来的操作步骤。对每个表，我们会推进最优的访问计划（消耗最小I/O的计划）。但局部的最优解未必是全局的最优解。有一些访问方案会产生一些特别的结果顺序，上层的操作会对这些顺序产生兴趣，即它们有称为全局最优解的可能性。令人关注的顺序是指一个表根据某个列通过以下方法之一排序：

• 使用ORDER BY
• 使用GROUP BY
• 使用还未衡量的join（在第一轮便指所有的join）

前两种的意义是显然的。最后一种也是有价值的因为它允许我们在后面的查询时使用排序归并连接来优化I/O消耗。全表扫描不会产生令人关注的顺序，因为结果是无序的。但索引扫描就能在索引建立的属性上产生顺序，从而能产生令人关注的顺序。当然，这种顺序只有在后面真正用到了才能算是“令人关注的”。

（这一段有点难懂。举个例子是三表连接时，前两表连接的最优解未必是三表连接的最优解。前两表如果用哈希连接，结果便是无序的。如果前两表使用排序合并连接，结果就是有序的。虽然会消耗比哈希连接更多的时间，但和第三个表连接时能用有序性进行优化，因此这两种连接方案都要保留。）

例：对于以下的查询语句：

SELECT *
FROM players INNER JOIN teams
ON players.teamid=teams.id
ORDER BY fname

有以下的访问方案（提到的I/O次数都是估计值）：

1. 对player全表扫描（100次I/O）
2. 对players.age索引扫描（90次I/O）
3. 对players.teamid索引扫描（120次I/O）
4. 对team全表扫描（300次I/O）
5. 对team.record索引扫描（400次I/O）

我们会将方案2、3、4推进至下一步。方案2、4分别为对于表访问的局部最优解。方案3会产生令人关注的顺序，因为teamid会被用于join，因此也会被推进至下一步。

6.第2—n轮操作

System R的接下来几轮的操作就是将各个表连接到一起。对第i轮，我们尝试用第i-1轮的结果和第一轮的某个表连接，从而实现将i个表连接到一起。例如我们在第二轮，将两个表进行连接，两个表都是第一轮的结果。在第五轮，我们将第四轮的结果（四个表的连接结果）和一个剩余的第一轮的结果进行连接，从而实现五个表的连接。这种手段是第二种启发性方向（左深计划）的应用，每次连接的一个来源都是基本表（的一部分）。

第i轮中我们会面对一个集合，集合中每个元素是所有表中选取的i个能不产生交叉连接而连接在一起的表集合。我们对这样的集合的每一个元素都会产生一个查询方案（假如如果有这样的元素）。和第一轮一样，我们会产生这一轮的最优解和能产生令人关注的顺序的解。当然当我们对各种连接方案进行估计时，我们假设数据库实现了这些连接方式。只有一种连接方式的结果是有序的：排序归并连接。所以唯一能产生令人关注的顺序的连接方法是在最后一次连接时使用排序归并连接（由于排序归并连接本身需要数据有序，所以前面的步骤中也要是令人关注的顺序，除非专门对结果进行排序）。排序归并连接的结果是在连接条件上有序的结果。

（各种连接方案，大体上分为三类：嵌套循环连接NLJ，即两层循环搜索，按照对内存的使用分为SNLJ、BNLJ、PNLJ，以及基于索引的INLJ；哈希连接HJ，即通过哈希表连接，有简单但低效的SHJ和复杂但有效的GHJ；排序归并连接SMJ，基于归并排序和双指针进行连接。）

例：对于以下三个表连接的查询：

SELECT *
FROM A INNER JOIN B
ON A.aid=B.bid
INNER JOIN C
ON B.bid=C.cid
ORDER BY C.cid

首先我们考虑会为哪些连接结果生成查询计划。我们只考虑{A,B}和{B,C}，因为这两组连接时不产生交叉连接。{A,C}不考虑，因为它们连接需要交叉连接（没有连接时的选择条件），而启发性方法要求避免交叉连接。为了简化问题，我们假设只实现了SMJ和BNLJ且第一轮都是全表扫描。有以下的连接方案（此处的I/O消耗仅是表现作用，实际研究中需要用选择性来计算）：

1. A BNLJ B(1000)
2. B BNLJ A(1500)
3. A SMJ B(2000)
4. B BNLJ C(800)
5. C BNLJ B(600)
6. C SMJ B(1000)

我们将方案1、5、6推进到下一步方案1和5分别是{A,B}和{B,C}连接的局部最优解；方案6会产生令人关注的顺序，因为有序的C.cid能被接下来的查询中使用到。方案3虽然也产生了顺序，但有序的是A.aid和B.bid，它们不会用于后面的查询，所以不是令人关注的顺序。它又比方案1的消耗大，故不考虑。

对第三轮，我们先考虑如下的连接方案：

1. JOIN 1{A,B} BNLJ C(10000)
2. JOIN 1{A,B} SMJ C(12000)
3. JOIN 5{B,C} BNLJ A(8000)
4. JOIN 5{B,C} SMJ A(20000)
5. JOIN 6{B,C} BNLJ A(22000)
6. JOIN 6{B,C} SMJ A(18000)

注意我们采用左深计划，因此连接顺序不能改变：左侧是连接结果，右侧是基本表。

我们推进的方案是2和3。3很显然，它是三表连接的最优解。2也是较优解因为它在C.cid上有序（别忘了后面还有个ORDER BY C.cid子句，它的代价还未计算）。方案2有序的原因是使用了B.bid=C.cid的连接条件，而且使用SMJ方案，故结果在C.cid是有序的。方案4和6在C.cid上不是有序的，因为连接条件不是C.cid，这两个方案的结果在A.aid和B.bid上是有序的，但我们后面需要的是C.cid有序，另两个属性有序没有用处。

7.计算连接操作的I/O消耗

当我们计算所需要优化的查询的I/O消耗时，需要考虑两个情况：

1. 是将先前的操作的中间结果进行持久化，还是将它们流式供给下一个操作的输入？
2. 是否从先前操作中获得的令人关注的顺序能在连接中减小I/O消耗？

因为这两个情况，我们不能直接套用前面的公式来进行计算。

7.1 第一种情况

为了将中间结果进行持久化，我们把中间结果写入磁盘（比如某个暂时性的文件），这是会产生额外I/O的过程。当数据被给予下一个操作时，又要从磁盘中读取到内存。另一方面，如果我们将一个操作的结果流入下一个操作，我们不向磁盘写入中间结果。每当我们在第一个操作中获得一个元组，它们会驻留在内存并给下一个操作。这个方案看似十分美好，但考虑到内存的有限性，它并不一定会比存储中间结果更优。

举个栗子，当我们提前选择操作和投影操作时，我们的目标是减小数据的规模，从而使我们在计划树上上升时能减少必要的I/O的数量。但是我们只能在选择或投影的结果被持久化或下一个操作对结果没有任何处理（比如S/P/BNLJ的左边关系、INLJ的左边的关系等）的情况下看到对I/O消耗的影响。我们来看一个具体的例子。

例：

（缓冲区Buffer，表示我们在数据库系统中进行计算的“内存”，和硬盘进行交互并向上层提供数据。它也以数据页为基本单位。我们用B表示缓冲区能存储的数据页数。用B表示缓冲区大小）

设B=5，有表P和T，[P]=50，[T]=100，P表中有30个数据页满足P.teamid>200，T表中有40个数据页满足T.tname>’Team5’，我们尝试对以下的查询进行优化：

SELECT *
FROM players P INNER JOIN teams T
ON P.teamid=T.teamid
WHERE P.teamid>200 AND T.tname>'Tname5';

首先假设优化器采用以下的查询计划：

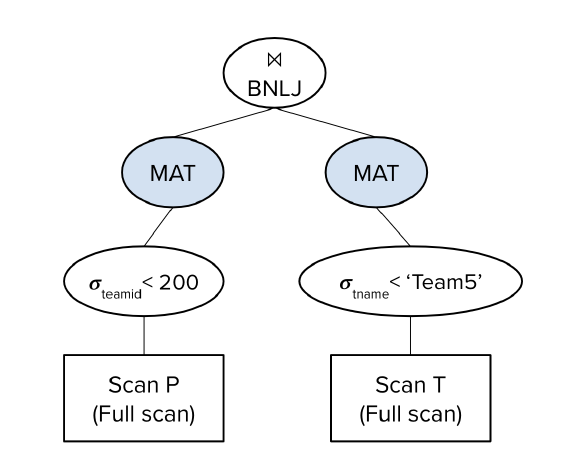
MAT的意思是将中间算出的数据持久化。这个计划预计的I/O消耗为:

$(50+30)+(100+40)+(30+\lceil\frac{30}{5-2}\rceil*40)=650$

我们首先对P进行全表扫描，读取50页，找出P.teamid>200的记录，将符合条件的30页记录P’写入磁盘。我们对T做同样的操作：读取100页，然后写入40页T’。

然后，我们用BNLJ将两个临时结果进行连接。我们先读取30页的P’，每次将B-2页放入缓冲区，然后逐个读取T’中的每页，寻找符合条件的连接记录。消耗为$(30+\lceil\frac{30}{5-2}\rceil*40)$次I/O。

接下来假设优化器用了下面一种查询计划：

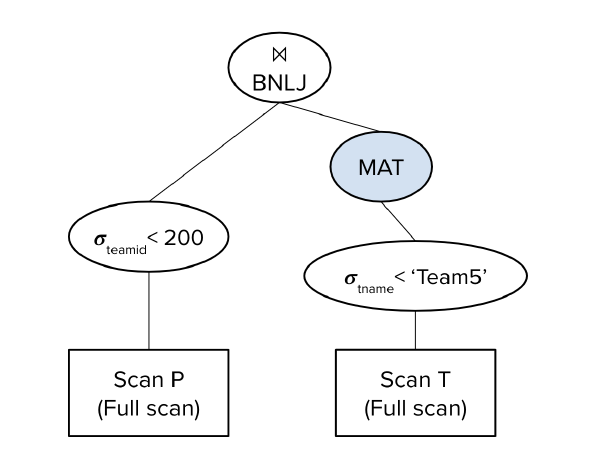
它和上面的区别是不将P处理的结果写入磁盘中。I/O消耗为：

$(100+40)+(50+\lceil\frac{30}{5-2}\rceil*40)=590$

我们首先读取100页T并将40页选择后的结果T’写入磁盘。然后全表扫描50页的P，这需要50次I/O。每当我们筛选出B-2页的符合条件的P’，我们就从T’中逐页取出进行比对。因此我们共比对$\lceil\frac{30}{5-2}\rceil$轮，每轮都读取40页T’。将所有消耗相加就得到了最终消耗。

接下来看另一种查询计划：

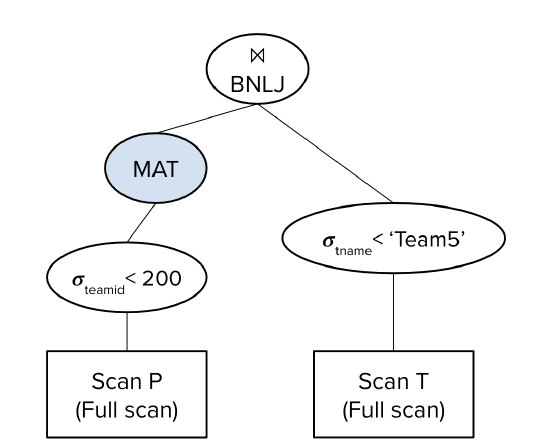
十分不可思议的是，它的I/O次数为：

$(50+30)+(30+\lceil\frac{30}{5-2}\rceil*100)=1110$

首先读取50页P，然后筛选出30页P’写入磁盘。随后我们读取P’，并且每读满B-2页就要从T中的对应记录进行连接。由于我们没有记录T’，因此对每一轮的B-2页P’，我们都要全表扫描，寻找可以连接且符合选择条件的记录。共比对$\lceil\frac{30}{5-2}\rceil$轮，每轮都全表扫描，消耗100次I/O。

（假如交换一下连接的顺序，变成T连接P，那么这里的I/O次数又该如何算呢？）

我们可以发现，即使我们把T的选择操作下移了，但他并没有产生优化的效果。它和下面的查询计划是等价的：

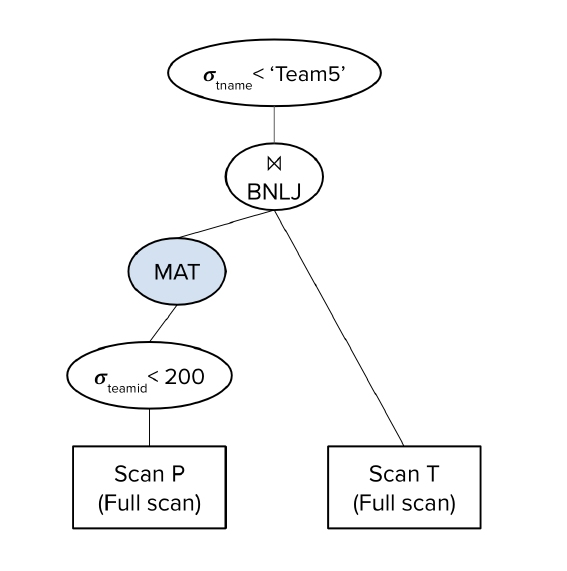
为什么I/O消耗没有减少呢？这是因为我们每次从T中获取数据时，我们都要扫描整个T表，而选择条件因为没有持久化到T’而没有生效。换句话说，对于前B-2页的P‘，为了连接扫描了100页T，虽然有了40页的T’，但这40页没有被持久化。到了下一轮B-2页的P’，仍然要重复扫描100页再筛选40页的过程。这说明选择和投影操作只有当下一个操作直接让数据通过（方案二的左侧）或中间结果被持久化（方案一、二的右侧）时才有意义。

再考虑最后一种方案：

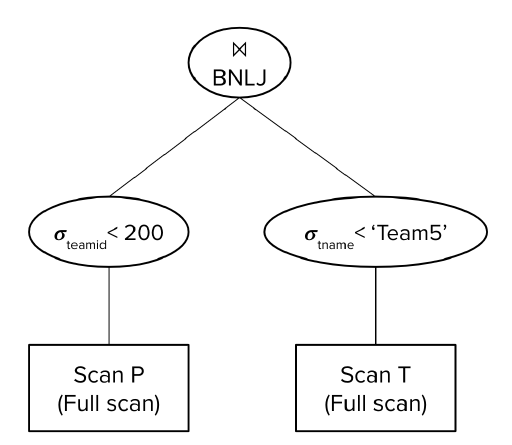
预计I/O数：

$50+\lceil\frac{30}{5-2}\rceil*100=1050$

首先对50页P全表扫描，每筛选出B-2页P’便全表扫描T一次。共全表扫描T$\lceil\frac{30}{5-2}\rceil$次。

可以看到，是否将某些中间数据持久化，会产生复杂的结果。

7.2 第二种情况

我们也要考虑从前面的操作中获得的令人关注的顺序的影响。例如我们要优化以下的查询：

SELECT * 
FROM players P INNER JOIN teams T
ON P.teamid=T.teamid
WHERE P.teamid>200;

假如我们把P.teamid>200前移，对P使用索引扫描消耗60次I/O，然后对T进行全表扫描需要100次I/O。索引扫描的结果会按照teamid排序，这是令人关注的顺序，因为它接下来会能用到P和T的连接上。

现在假如我们用SMJ作为连接策略，我们可以计算出I/O消耗为：给P排序的消耗+给T排序的消耗+(50+100)。最后一项是双指针遍历P和T的消耗。由于我们使用了索引扫描P，因此此处给P排序的消耗为0，而是要计算索引扫描P并将结果流入连接阶段的消耗。因此总预计消耗为(给T排序的消耗+60+100)次I/O。