概述
数据流分析解答的是“数据如何在控制流图(CFG)上流动”的问题。而这里的“数据”具体而言就是指程序特有的数据,在CFG上流动便是指流过其节点与边。“数据”代表的是抽象手段,而“流过”代表的是近似手段。
may analysis
输出可能为真的结果(过近似 over-approximation)
只要有一种为真的可能就应输出
must analysis
输出一定为真的结果(欠近似 under-approximation)
只有全部情况下为真才能输出
无论哪种近似手段,都是追求safe的近似。
在节点上,我们使用转移函数(Transfer function)的方式,而在边上,我们使用控制流处理(Control-flow handling)的方式。
对于不同的数据流分析应用,都有不同的数据抽象、流近似、转移函数和控制流处理。
在基本的数据流分析中,我们不考虑方法调用和别名这两种情况。
基础概念
输入状态和输出状态
每一条IR语句都将一个输入状态转变为一个新的输出状态。这两种状态与语句执行前后的程序状态关联。
显然的,对于相邻的两条语句,第一条语句的输出状态和第二条语句的输入状态是相等的。
值得注意的是,当两条控制流汇聚到一条语句时,我们使用$\wedge$来表示结果。这个运算根据应用来定义。
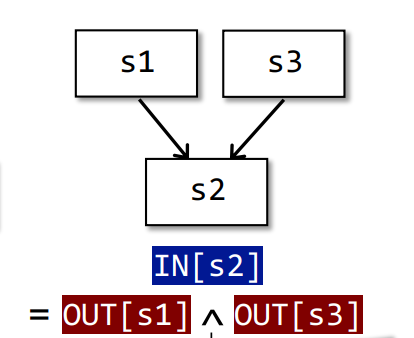
在所有数据流分析的应用中,我们把每一个程序点(program point)关联于一个数据流对象来表示这个点时所有可能程序状态的抽象。
而数据流分析的目的是通过预先设定的规则来对所有语句的输入、输出状态进行求解。这种规则基于安全近似导向的约束,其基于语句的语义(转移函数)和控制流。
转移函数约束
正向分析:
\[OUT[s]=f_s(IN[s])\]反向分析:
\[IN[s]=f_s(OUT[s])\]控制流约束
在有n条语句的基本块内:
\[IN[s_{i+1}]=OUT[s_i],i=1,2,......,n-1\]基本块之间:
\[IN[B]=In[s_1]\\ OUT[B]=OUT[s_n]\\\]这两句揭示了基本块和具体语句的状态关系
\[OUT[B]=f_B(IN[B]),f_B=f_{s_n}\circ...\circ f_{s_1}\\ IN[B]=\bigwedge_{P\ a\ predecessor\ of\ B}OUT[P]\]这两句揭示了正向分析中基本块间的状态关系
\[IN[B]=f_B(OUT[B]),f_B=f_{s_1}\circ...\circ f_{s_n}\\ OUT[B]=\bigwedge_{S\ a\ successor\ of\ B}IN[S]\]这两句揭示了反向分析中基本块间的状态关系
Reaching Definitions
定义
在程序的p点上的定义d到达了程序的q点。所谓到达,就是指存在一条路径,其没有出现重复定义(没有被新的定义kill掉)
该分析的经典应用是检测未初始化变量。如果未初始化定义能够到达目标点,那么就有使用未定义变量的风险。
抽象
程序中所有的定义可以用一个位向量来表示。
如D1,D2,…,D100(100个定义),可以用00000……00(100位)表示。第i位表示Di定义
转移函数
对于以下语句:
D: v = x op y
这句产生了对变量v的定义D,同时消灭了其他对v的定义,而x和y的定义状态不受影响。
于是我们得到转移函数
\[OUT[B]=gen_B \cup (IN[B]-kill_B)\]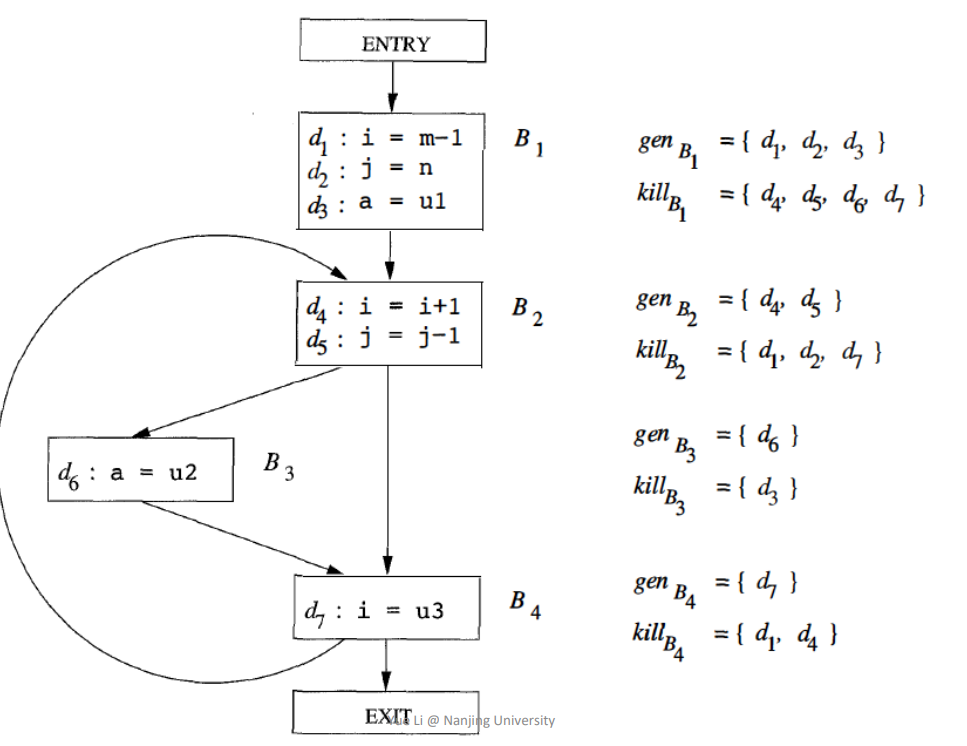
控制流
某个定义只要有一条道路能到达,那么它就是可达的,即有:
\[IN[B]=\bigcup _{P\ a predecessor\ of\ B}OUT[P]\]算法
输入:CFG(每个基本块的$kill_B$和$gen_B$都已算出)
输出:每个基本块的IN[B]和OUT[B]
方法:
OUT[entry] = EMPTY
for(each entry block B\entry)
OUT[B] = EMPTY; //may analysis一般为EMPTY, must analysis一般为FULL
while(changes to any OUT occur)
for(each basic block B\entry){
IN[B] = union(OUT[B.predecessors]);
OUT[B] = union(gen(B), IN[B]-kill(B));
}
该迭代算法的结构也是很多分析算法的模板。
例如对以下程序:
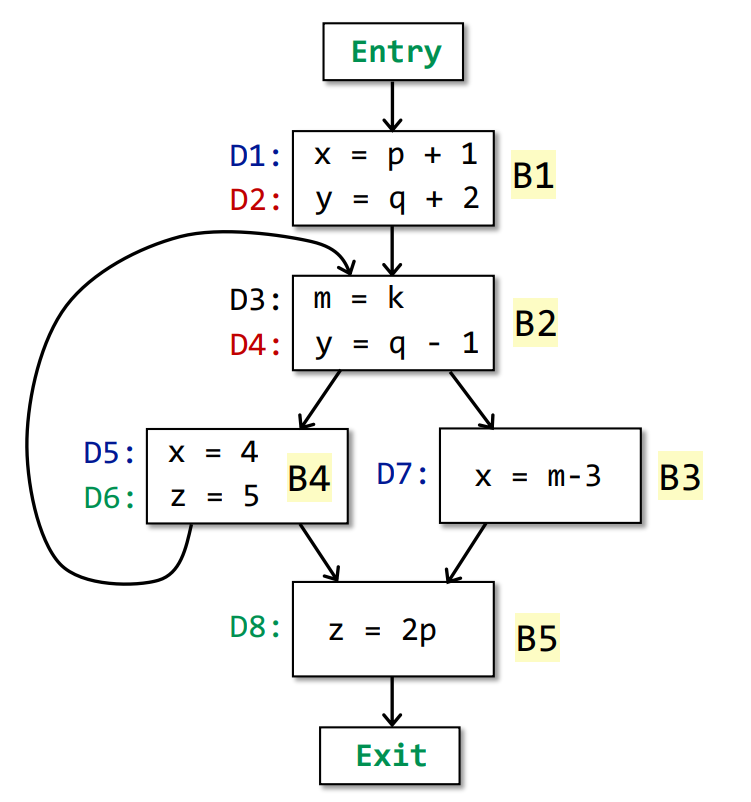
我们用八位向量表达一个状态,每位表示对应的定义的存活情况。
初始时,所有OUT均被初始化为00000000
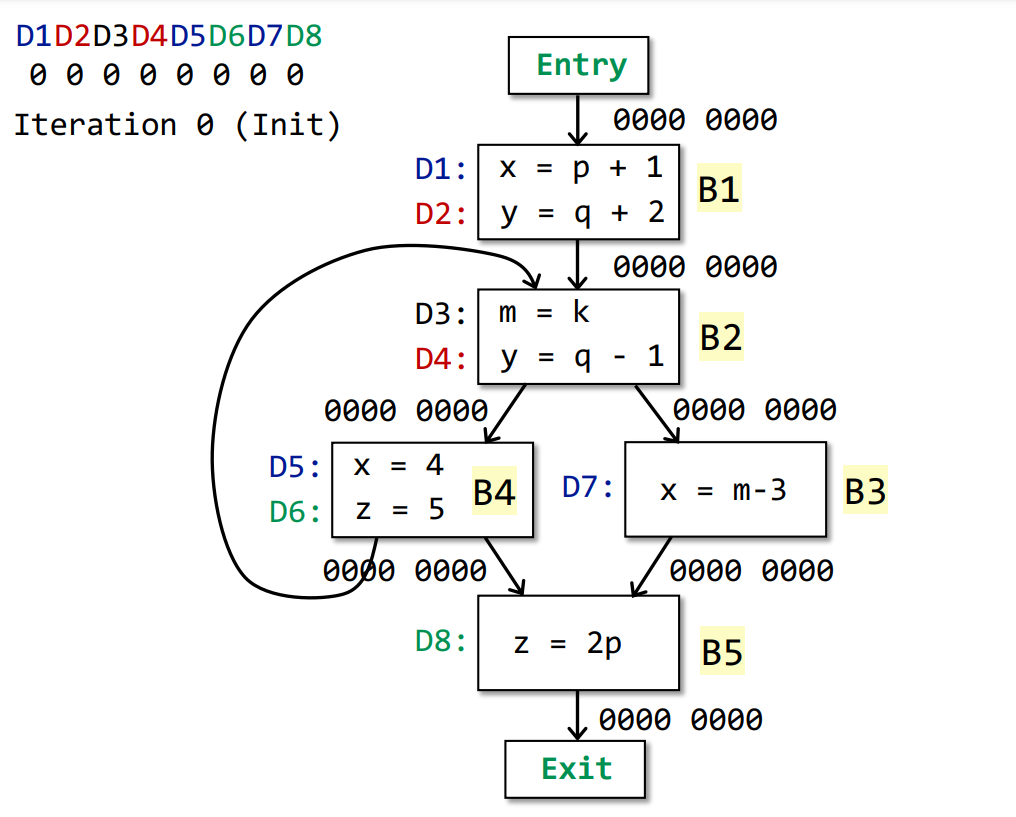
第一轮迭代中,B1首先产生1100 0000的OUT,随后B2的IN为B1和B4的OUT的并集,即为1100 0000。B2生成D3和D4,消灭D2,OUT为1011 0000。随后B3和B4分别输出0011 0010和0011 1100(B3和B4的计算顺序不影响最终结果)。B5输入0011 1110,输出0011 1011,第一轮迭代结束。
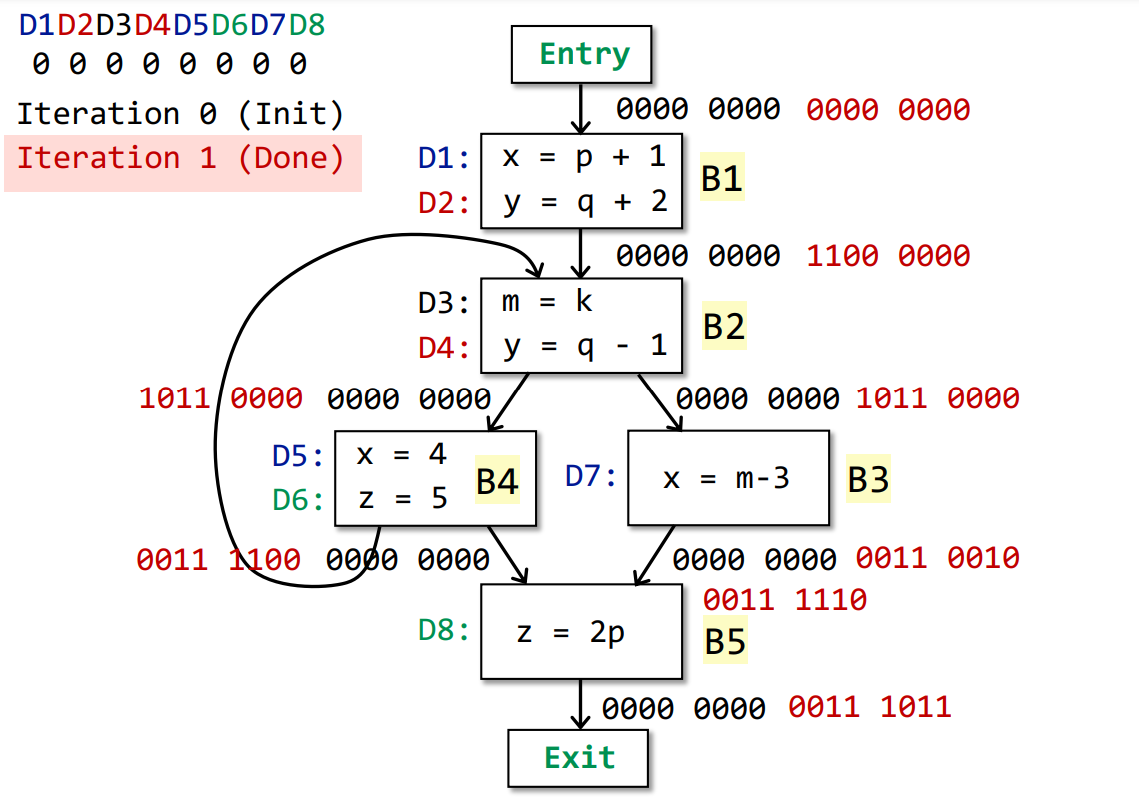
在第一轮迭代中,存在基本块的输出发生了变化,我们开始新一轮迭代。
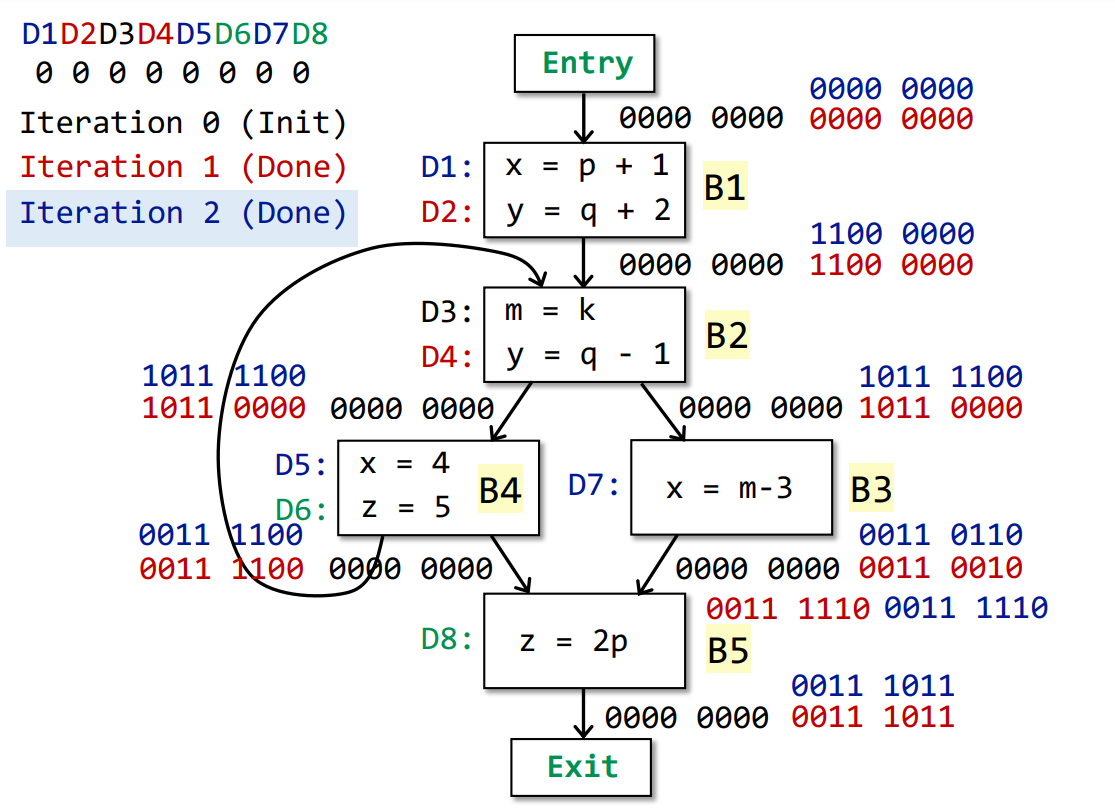
在第二轮迭代中,B2和B3的输出发生了变化,进行第三轮迭代。
在第三轮迭代中,所有基本块的输出未发生变化,迭代结束。
在第三轮迭代中,我们可以发现,当IN[B]不变时,OUT[B]是不变的。
解析
为什么该算法能够停止
对于转移函数
\[OUT[B]=gen_B \cup (IN[B]-kill_B)\]gen和kill是和in与out无关的,在分析过程中保持不变。于是当in不变时,out便不变。
当某个点的IN中的某个值变成1后,它在之后的相同位置的IN便永远都会变成1。于是输出便会最终固定。而位数是有限的,便会最终到达一个不动状态。
终止条件是否正确
当达到终止条件后,再次迭代已经不会改变任何状态。因为
\[OUT[B]=gen_B \cup (IN[B]-kill_B)\]如果IN不变,OUT就不变。
\[IN[B]=\bigcup _{P\ a predecessor\ of\ B}OUT[P]\]如果OUT不变,IN就不变。
