很多时候我们面对的是十分“稀疏”的数据——图数据。

图数据处理在网页权重排序、社交检测、灌水检测等方面发挥重要作用。

新型数据——图数据

图数据在各种地方存在。例如社交网络（著名的六度分割理论，在Facebook社交图谱上只需四度多）、媒体网络（政治博客的关联）、信息网络（科技领域的交错关联、网络拓扑）、技术网络（七桥问题）。

将Web表示为图

Web表示为有向图：

• 节点：网页
• 边：超链接

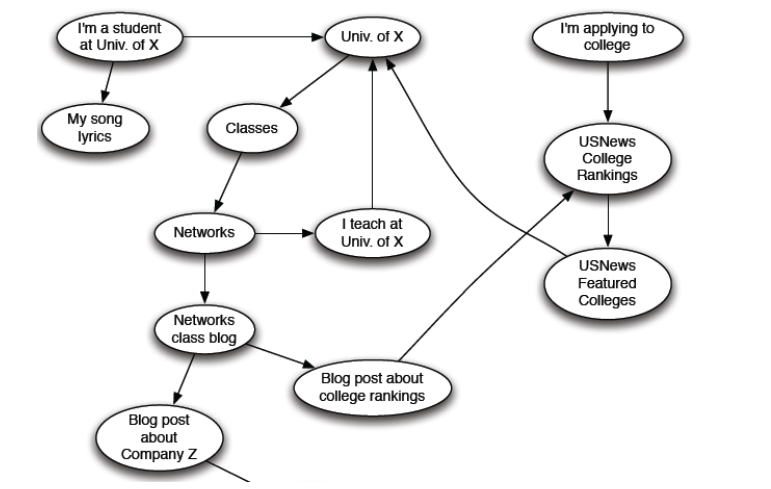
网页组织与检索

方式一：网页索引（人工编辑）

Yahoo、DMOZ、LookSmart等早期网页的方法，效率低

方式二：Web搜索

问题：网络充满了不可信、过时和随机的东西

网页搜索的挑战

• 网络中存在多个来源的数据，如何判断可信度？

  可信的页面彼此相互引用和链接

• 查询“数据”的最佳回答是什么？

  实际关于“数据”的页面往往指向很多“数据”

结果：所有网页的重要性不是平等的，可用通过链接结构对页面进行排序。

链接分析方法

Page Rank

Idea：链接投票

• 页面拥有的入链越多越重要
• 来自重要的链接占最大权重

对于以下图：

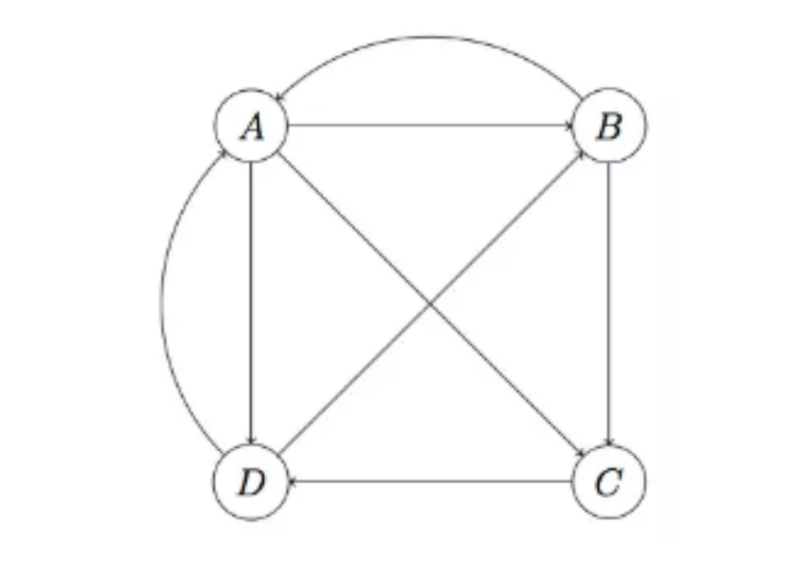
可以计算跳转概率矩阵

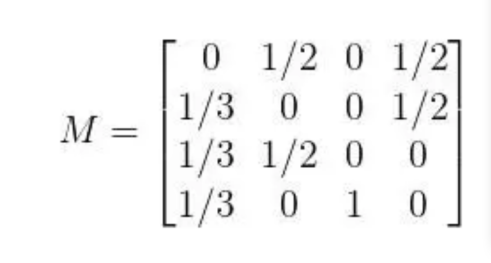
$M_{ij}$表示从页面$J$跳转到界面$I$的概率

原始rank：

相乘得到第一次的权重更新：

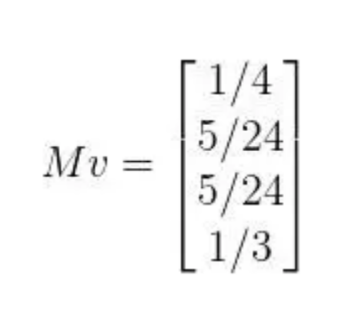
在一次迭代后，转移矩阵不变，用更新后的权重继续与其相乘，直至达到收敛条件。

一些特殊情况：

Dead end：

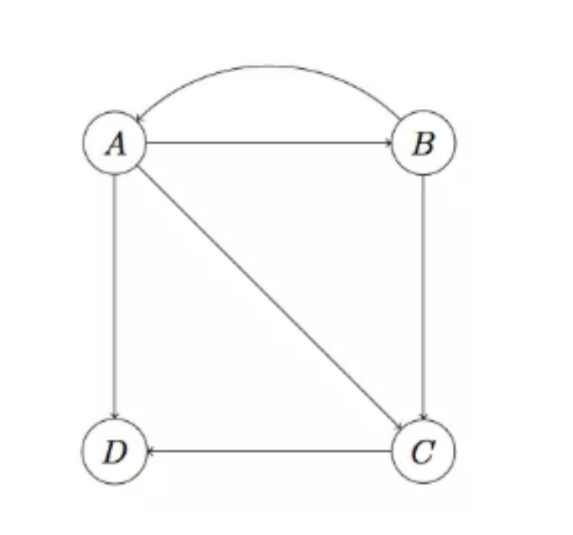
在这种情况中，D为Dead end，A、B、C的权重会在迭代中完全流至D。

处理方法：把D移除，此时C也成为了Dead end，也要去除。

Spider Traps：

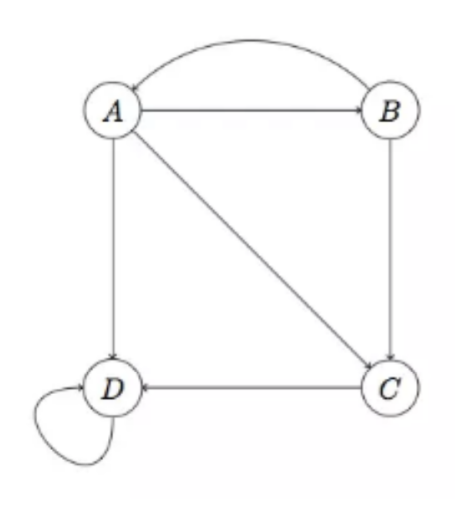
在这种情况中，D的出链不为0，但A、B、C的权重也会全部流向D。

解决方法：修改初始的M，令$M=\beta M+(1-\beta )\frac{ee^T}{n}$，$1-\beta$为随机打开其他网页的概率

Page Rank算法中每次迭代中，页面$j$的rank $r_j$： \(r_j = \sum_{i → j}\frac{r_i}{d_i}\) $d_i$为节点i的出度。

求解的流等式为：$r=M · r$，可见$r$为$M$的一个特征向量，且1为$M$的主特征值，此时可以通过Power Iteration算法求解$r$。

Power Iteration算法：

• 初始：$r^{0}=[1/N,…,1/N]^T$

• 迭代：$r^{t+1}=M·r^t$

• 终止：$\mid r^{t+1}-r^t\mid_{1}<\varepsilon$

  其中$\mid r \mid$为$r$的$L1$正则化（由于$\sum r_i$总和始终为1，所以不变）

算法的正确性证明是较为简单的线性代数问题，读者可自行证明。