决策树
决策树是解决分类问题的方法之一。
形状
一棵多叉树,每个内部节点表示一个特征,叶节点表示一个类
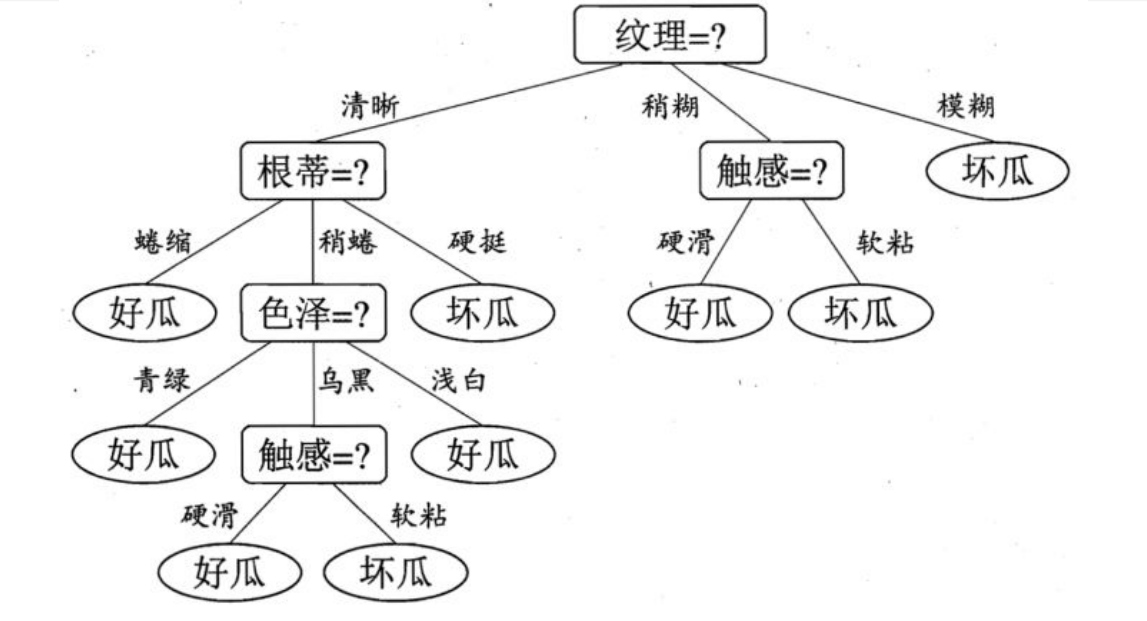
假如有一个纹理清晰,根蒂硬挺的瓜,我们首先通过纹理到达“根蒂=?”这一节点,然后通过根蒂到达”坏瓜”这一节点,得出这是一个坏瓜的决策。
ID3算法
- 对所有没有使用的属性计算样本在这个属性的信息熵
- 选取其中熵最小的属性
- 生成包含该属性的节点
信息熵
设集合D中第k类占比为$p_k$,则D的信息熵为:
\[Ent(D)=-\sum_{k=1}^K p_klogp_k\]一般而言,信息熵越低,代表其信息量越大。
信息增益
信息增益是针对一个分支标准T,引入该分支比不引入的信息熵差异
\[Gain(D,a)=Ent(D)-\sum_{v=1}^V\frac{\mid{D^v}\mid}{\mid{D}\mid}Ent(D^v)\]示例
对于一批瓜
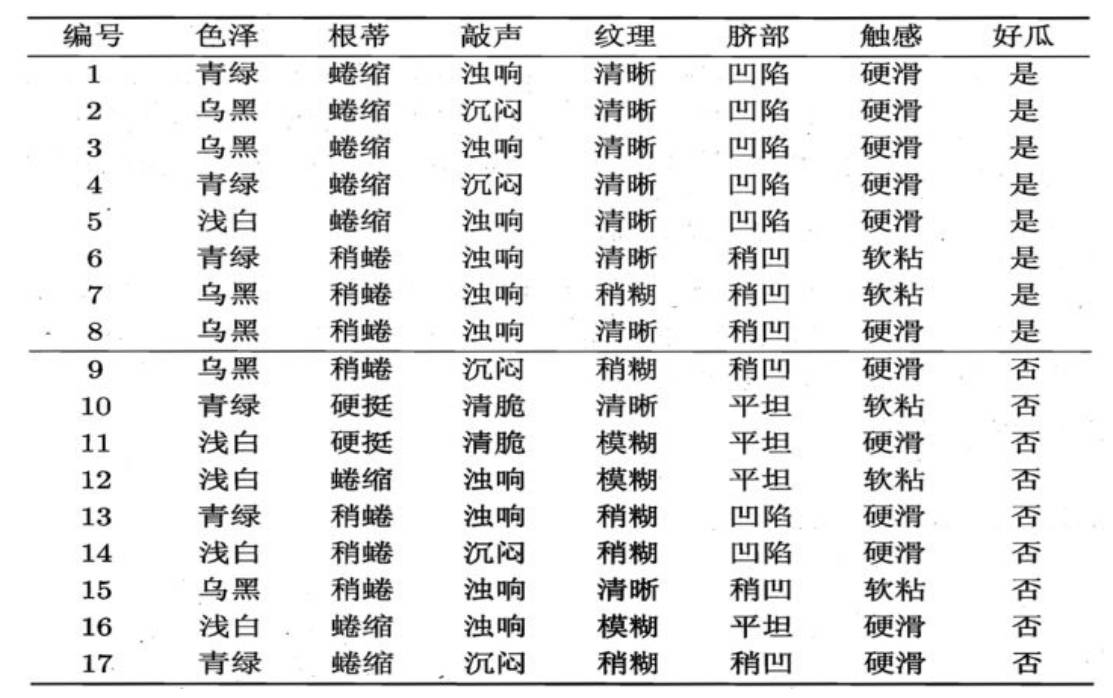
我们首先计算整体的信息熵(p为是否是好瓜)
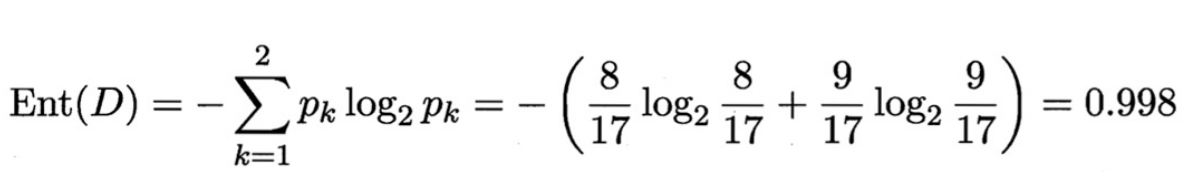
然后计算色泽、根蒂、敲声、纹理、脐部、触感各个属性的信息增益。以色泽为例。
色泽有三个可能取值。
- D1(青绿)有六个瓜,好坏各有3个
- D2(乌黑)有六个瓜,好瓜4个,坏瓜2个
- D3(浅白)有五个瓜,好瓜1个,坏瓜4个
随后对每个集合Di计算各自的信息熵
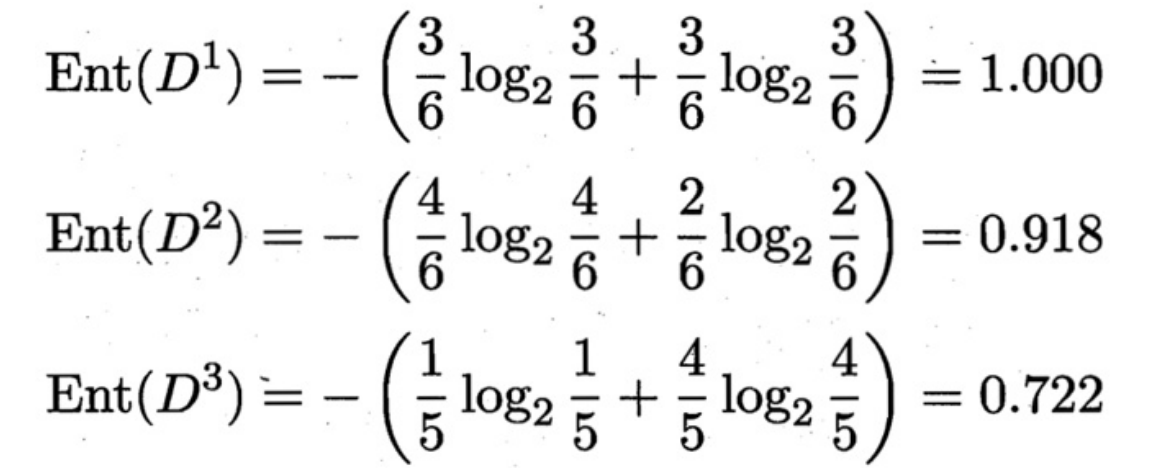
随后计算色泽的信息增益
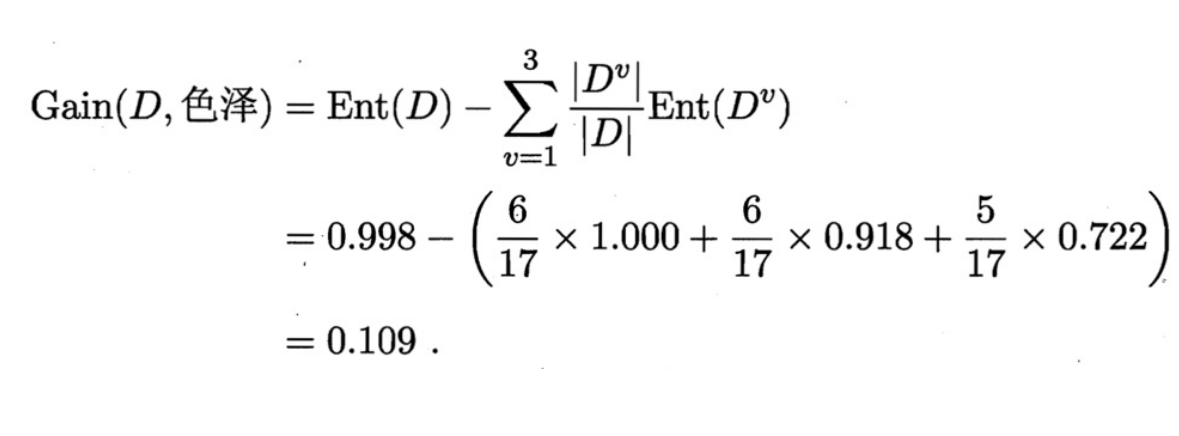
同理可算出其他属性的信息增益

显然纹理属性能带来的信息增益最大,即引入后信息熵降低最大,便是我们优先考虑的决策属性。
划分完纹理后,我们得到了第一层划分
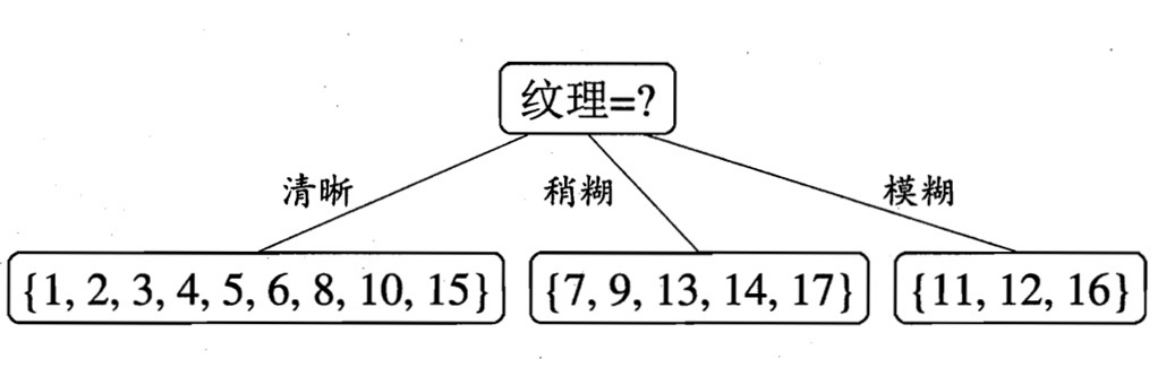
我们可以对每个子集合重复上面的步骤,例如对清晰的瓜进行计算得到
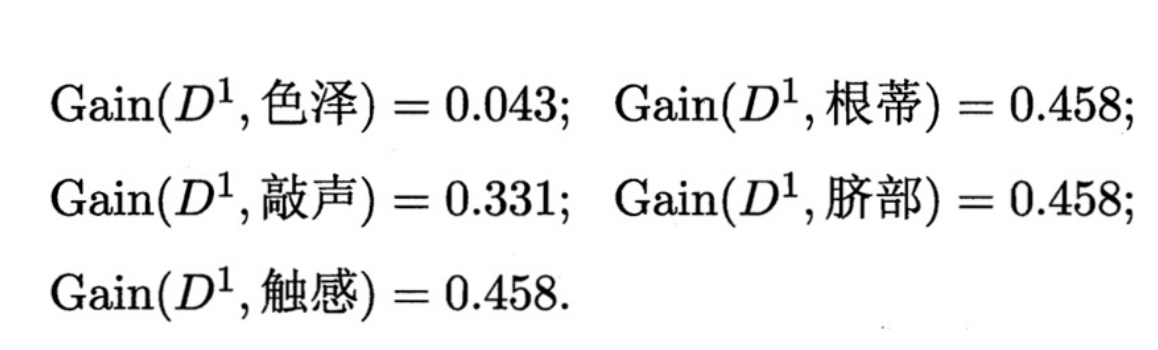
在三个最高者中任选一个,得到D1的下一层。
对其他子集和深层的计算同理。
缺点
- 偏好可取值较多的属性,例如有三个取值的纹理属性(极端情况下是唯一取值的”编号”属性)
- 不能处理连续属性
C4.5算法
信息增益率
\[Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}\\ IV(a)=-\sum_{v=1}^V\frac{\mid{D^v}\mid}{\mid{D}\mid}log\frac{\mid{D^v}\mid}{\mid{D}\mid}\]通过除以IV,可取值较多的属性被限制,但可取值较少的属性被偏好。
C4,5算法先从候选划分属性中选择信息增益率高于平均水平的属性,再从中选择信息增益率最高的
处理连续属性
对有m个值的连续特征A,中间切分出m-1个切分点(取左右两个值的均值)。然后选择信息增益率最高的切分点来进行分类。
CART算法
步骤
- 将样本递归划分进行建二叉树过程
- 用验证数据进行剪枝
KNN算法
对新的样本,将其与训练集中所有样本的距离进行计算并排序。取其中前K近的样本,其中占多数的类别就是新的样本的分类。
距离函数
常用的距离函数为欧式距离
组合函数
在计算前K近的样本中各个分类的占比时,有两种组合方式
- 民主投票:每个邻近样本的权重是一样的
- 加权投票:每个邻近样本的权重是不一样的,一般采取权重和距离成反比来计算
集成分类
通过将多个分类器聚集在一起来提高分类的准确性和模型的稳定性。集成分类器有训练数据构建一组基分类器,通过对每一个基分类器的预测投票来决定种类
构建分类器的过程中,一般有两种集成方法,一种是使用训练集的不同自己训练得到不同的基分类器,另一种是使用同一个训练集的不同属性自己训练得到不同的基分类器。
构建方法
处理训练数据集
对原始数据进行再抽样来得到多个数据集。常用的方法有装袋和提升
处理输入特征
根据原始数据的各个特征进行划分数据集。典型例子是随机森林
处理类标号
适用于类数足够多的情况
处理学习算法
在同一个训练集上执行不同算法得到不同模型
优缺点
优点:克服了单一分类器的缺点,如对样本的敏感性,难以提高精度等
缺点:必须保证各个基分类器之间完全独立
指标
分类准确率、计算复杂度、可解释性、可伸缩性、健壮性、不平衡数据分类
混淆矩阵
包含正类预测为正(TP)、负类预测为正(FP)、正类预测为负(FN)、负类预测为负(TN)
分类准确度:
\[Acc=\frac{(TP+TN)}{C}\]错误率:
\[Err=1-Acc=\frac{(FN+FP)}{C}\]精度
\[p=\frac{TP}{(TP+FP)}\]召回率:
\[r=\frac{TP}{(TP+FN)}\]F1:
\[F_1=\frac{2rp}{(r+p)}\]