迭代算法与单调性
\[init \rightarrow (\perp,\perp,...,\perp)=X_0\\iter\ 1 \rightarrow (v_1^1,v_2^1,...,v_k^1)=X_1=F(X_0)\\iter\ 2 \rightarrow (v_1^2,v_2^2,...,v_k^2)=X_2=F(X_1)\\...\\iter\ i \rightarrow (v_1^i,v_2^i,...,v_k^i)=X_i=F(X_{i-1})\\iter\ i+1 \rightarrow (v_1^i,v_2^i,...,v_k^i)=X_{i+1}=F(X_i)=X_i\\\]对于以上过程,我们希望迭代最终达到不动点。不动点定理需要满足两个条件:迭代单调、格有限。
乘积格和域保证了格的单调性,所以我们要证明迭代是单调的。
每次迭代相当于执行一次函数F,其中包含转移函数和合并函数。
一般的gen/kill函数是单调的。对于转移函数$\sqcap / \sqcup$,我们首先可以证明:
\[\forall x,y,z \in L,x\sqsubseteq y \rightarrow x\sqcup z \sqsubseteq y \sqcup z\]即$\sqcup$是单调的,同理$\sqcap$也是单调的。便可证明一般的转移函数$L\times L \rightarrow L$是单调的,于是便有迭代是单调的。
迭代长度
我们定义一个格中最小元素到最大元素的最长距离为格的高$h$
假设一个node需h次迭代到达顶部。
考虑最坏情况,每次迭代只有一个node发生了最小改变,则需要$h*k$次迭代才能到达全部node的不动点
Reaching Definitions
作为May analysis,其是要实现unsafe result向sale result。
在该分析中,我们将全部节点初始化为全0,即所有def都没有reach。迭代的过程,就是在格中不断上升的过程。
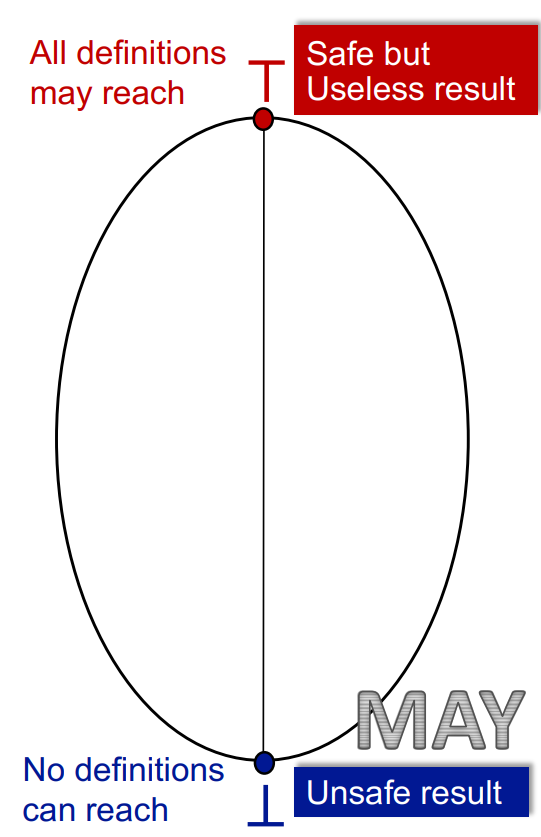
而完全正确的结果在格中的某处,在其下的部分都是unsafe的结果,在其上的都是safe的,但用处逐渐减弱的结果。
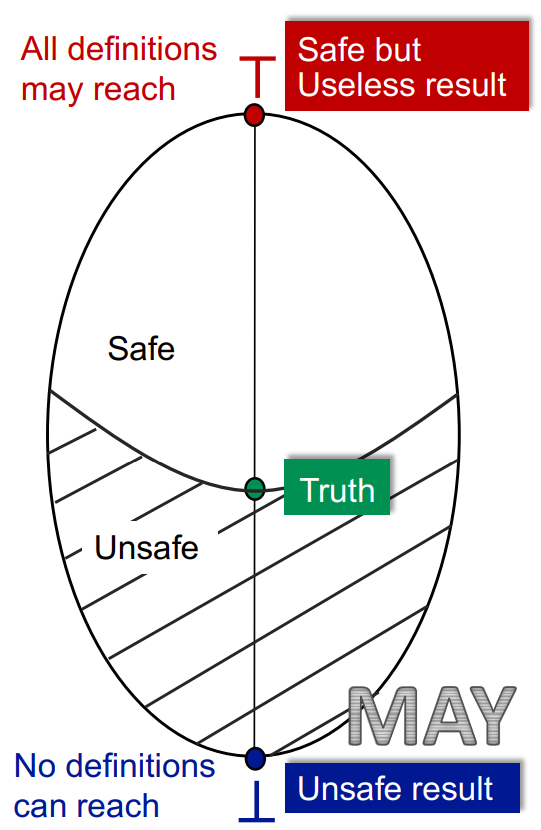
而通过人为设计的safe转移与合并,我们可以保证最终能越过Truth到达safe的地区。
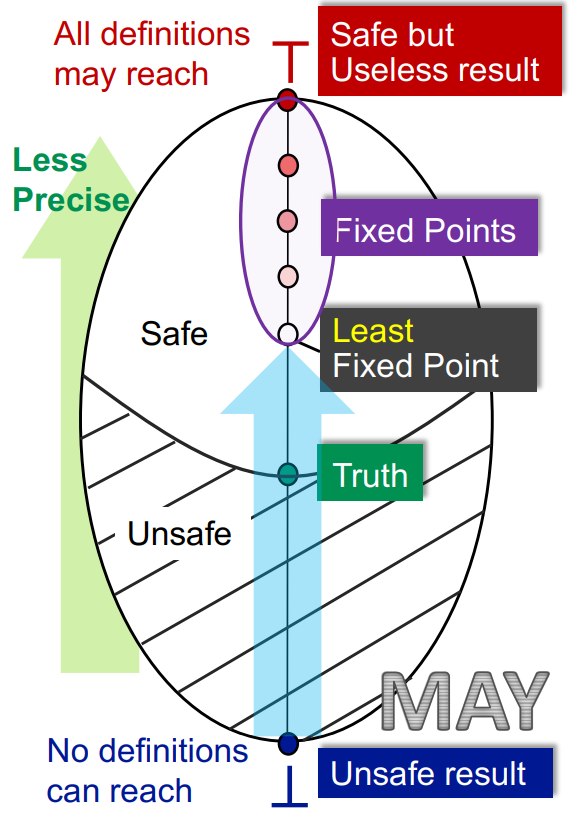
通过到达最小不动点,我们就能得到最精确而最靠近事实的结果。但不动点的位置是根据设计的迭代函数来得出的。
Available Expression
作为Must analysis,则是初始化为最大,从上向下移动
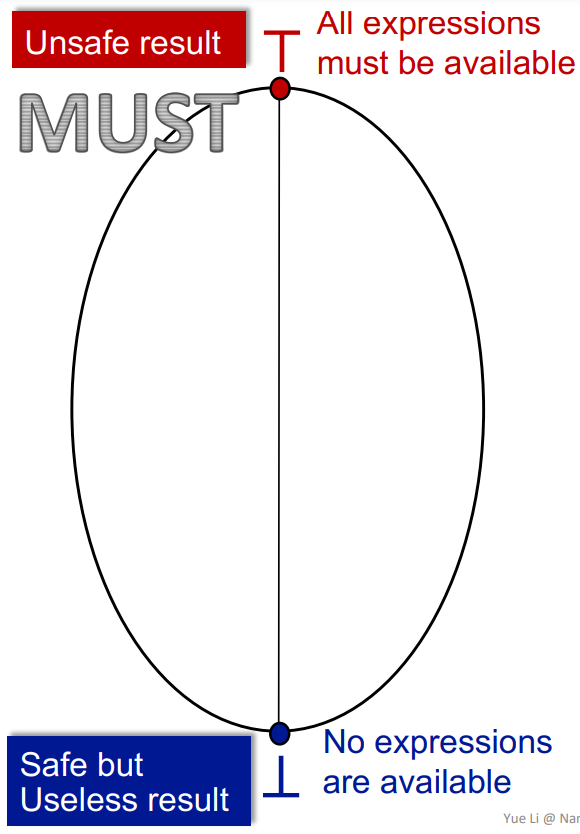
其向下走达到最大不动点。
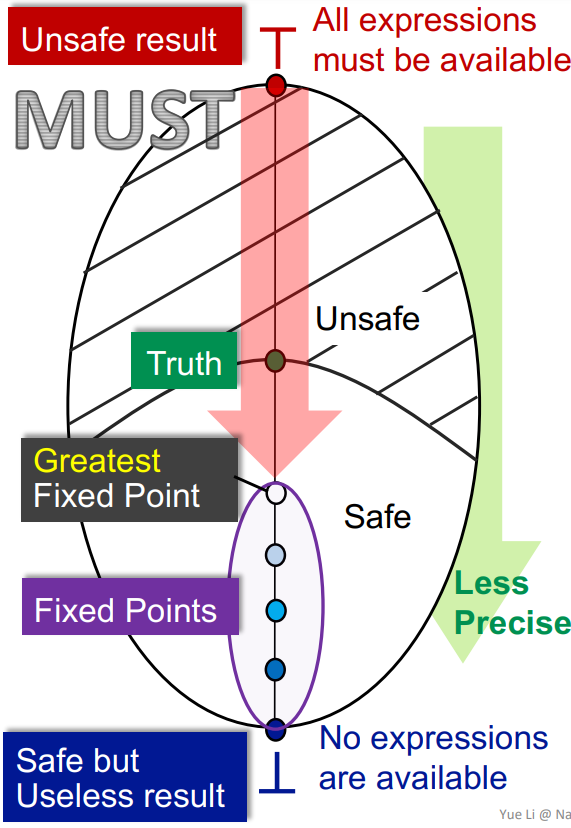
解的精度
MOP
Meet-Over-All-Paths Solution,是衡量精度的指标
设一个Node为$Entry \rightarrow s_1\rightarrow s_2 \rightarrow … \rightarrow s_i$,有各自的转移函数
则有
\[MOP[s_i]= {\sqcap /\sqcup}_{A \ path \ P \ from \ Entry\ to\ S_i} F_P(OUT[Entry])\]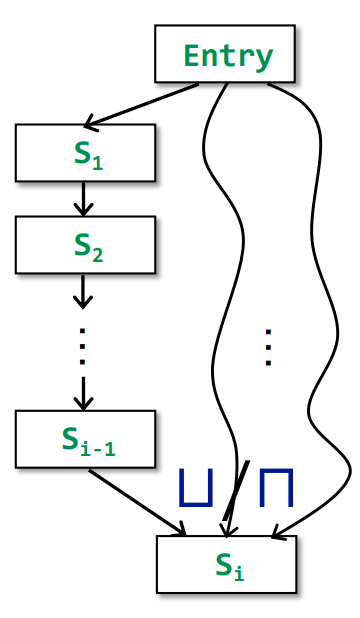
其中一些路径在实际中可能不会执行,导致结果不够精确。
实际路径是无法数尽和展开(循环)的,导致MOP实际运用不足。
迭代算法和MOP的比较
以以下为例
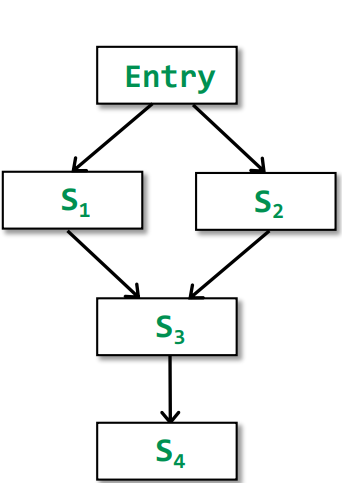
从迭代算法的角度,有:
\[IN[s_4]=f_{s_3}(f_{s_1}(OUT[entry])\sqcup f_{s_2}(OUT[entry]))\]从MOP的角度有:
\[MOP[{s_4}]=f_{s_3}(f_{s_1}(OUT[entry]))\sqcup f_{s_3}(f_{s_2}(OUT[entry]))\]进行简化则是:
- 迭代:$F(x\sqcup y)$
- MOP:$F(x)\sqcup F(y)$
我们可以证明$F(x)\sqcup F(y) \sqsubseteq F(x\sqcup y) $,即迭代算法不比MOP更精准。当F满足分配律时,迭代算法和MOP的精准度相同。而位向量+gen/kill的分析是满足分配律的。
常量传播
给定程序某个点p处的变量x,判断该变量x是否为一个常量值。
抽象
使用一系列(x,v)的集合来表示每个节点的输出。x为常量时v为其值,不是常量时v为NAC。
格
V的域:
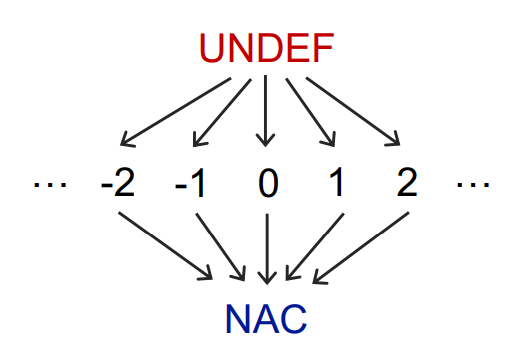
合并符号$\sqcap$:
- $NAC\sqcap v = NAC$
- $UNDEF\sqcap v=v$
- $c_1\sqcap c_2=NAC$
- $c\sqcap c=c$
转移函数
对于
s: x = ...
有转移函数
\[F=OUT[s]=gen\cup (IN[s]-\{(x,\_)\})\]不同的s的情况
- x = c gen = {(x, c)}
- x = y gen = {(x, val(y))}
- x = y op z gen = {(x, f(y, z))}
- y、z均为常量:f(y, z) = val(y) op val(z)
- y或z不为常量:f(y, z) = NAC
- 其他情况:UNFEF
工作集算法
其是迭代算法的变体。以向前的May analysis为例
OUT[entry] = EMPTY;
for(each entry block B\entry)
OUT[B] = EMPTY;
Worklist = allBlocks;
while(!Worklist.empty())
B = Worklist.get();
old_OUT=OUT[B];
IN[B] = union(OUT[B.predecessors]);
OUT[B] = union(gen(B), IN[B]-kill(B));
if(old_OUT != OUT[B])
Worklist.add(B.predecessors);
