Live Variables Analysis
定义
某个在p点定义的变量v是否在p点之后的某条路径中被用到了,也就是定义v和使用v之间其不应被重新定义。如果用到了,那么其就是在p点存活的。
抽象
程序中所有的变量可以用一个位向量来表示。
如D1,D2,…,D100(100个变量),可以用00000……00(100位)表示。第i位表示Di变量
转移函数
对于该分析,我们采取反向分析的手段,从程序结尾向开头计算。
对于语句
D: v = x op y
其产生了x和y的use,并且kill了下面的v(的使用),上方的v到这句便不再存活。
也即 \(IN[B]=use_B \cup (OUT[B]-def_B)\)
控制流
我们可以看出块间转移函数: \(OUT[B]=\bigwedge_{S\ a\ successor\ of\ B}IN[S]\)
即只要有一条路径中使用到了某个变量,那么它就应该是存活的
算法
输入:CFG(每个基本块的$def_B$和$use_B$都已算出)
输出:每个基本块的IN[B]和OUT[B]
方法:
IN[exit] = EMPTY
for(each entry block B\exit)
IN[B] = EMPTY;
while(changes to any IN occur)
for(each basic block B\exit){
OUT[B] = union(IN[B.successors]);
IN[B] = union(use(B), OUT[B]-def(B));
}
相对于之前的模板,其作为反向分析,对IN和OUT进行了相关替换。
例如在以下程序
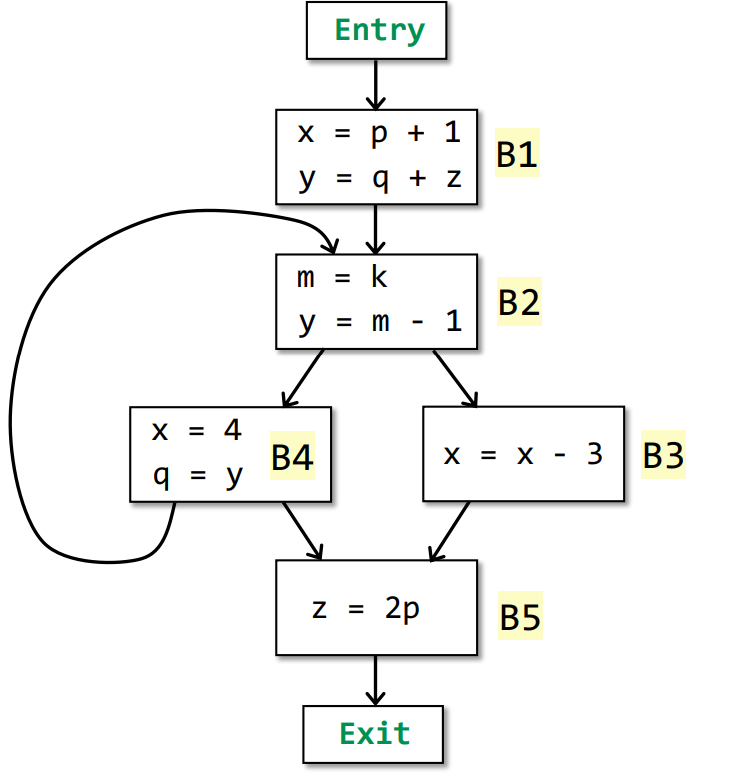
我们经过一轮迭代可以得到
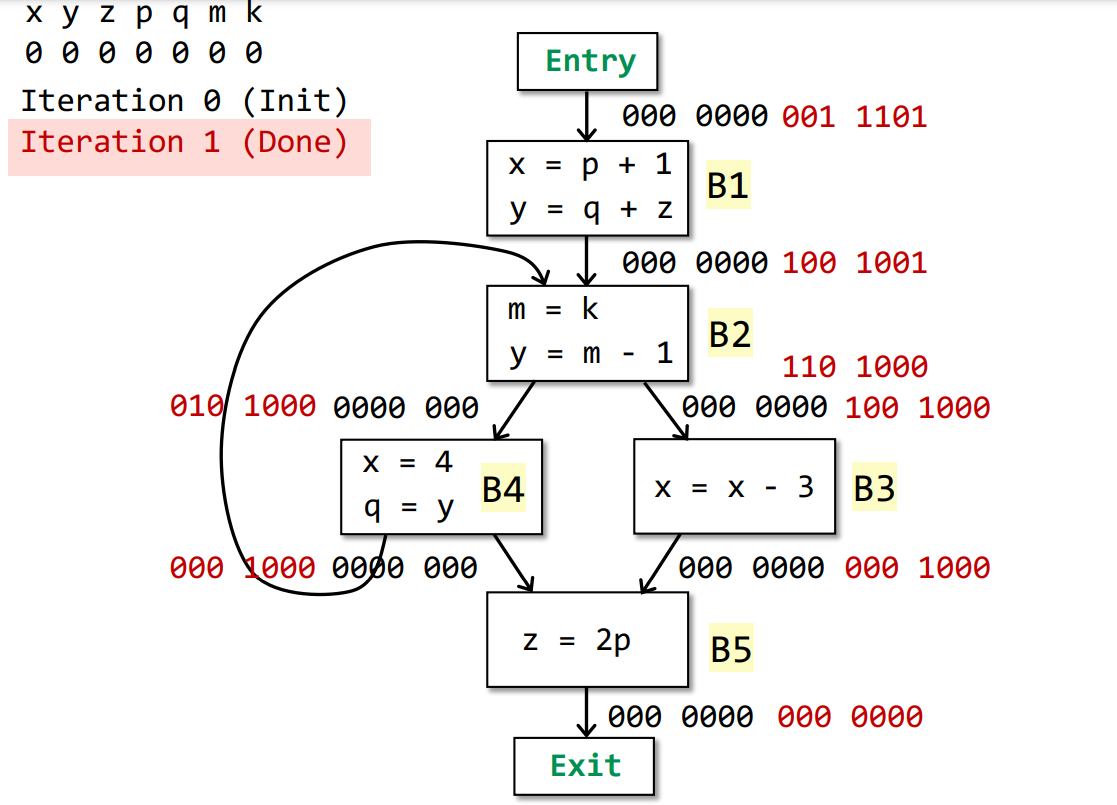
第二轮迭代
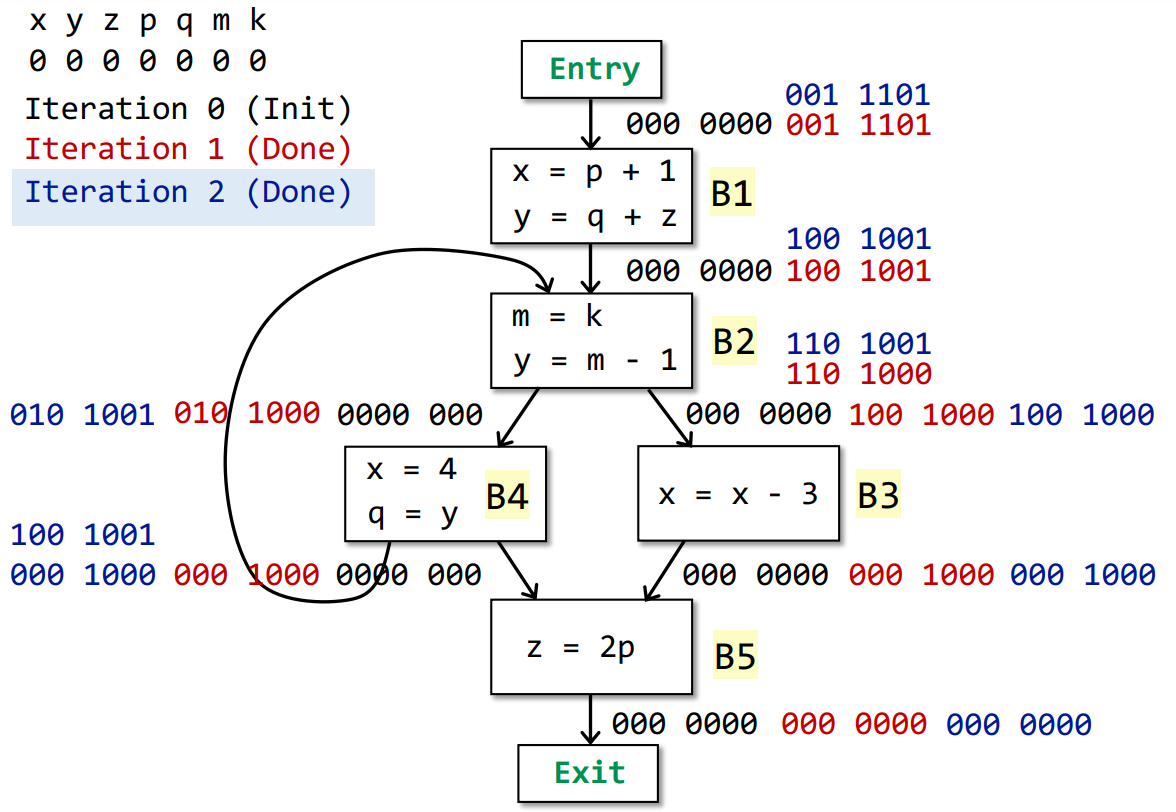
第三轮迭代没有变化,结束。
Available Expression Analysis
定义
对于一个p点的表达式x op y,如果所有从开头到p的路径都计算了这个表达式,且在在最后一次计算后,没有对x和y的重复定义,那么这个表达式在p点就是可用的。
这个分析可以帮助我们将对x op y的重复计算进行替换。
抽象
同理使用位向量。
转移函数
对于语句
D: v = x op y
其产出了表达式x op y,消灭了所有包含v的表达式。
对于基本块,有 \(OUT[B]=gen_B \cup (IN[B]-kill_B)\)
控制流
该分析为must analysis,所以我们需要使用并集来进行基本块的归并。 \(IN[B]=\bigcap _{P\ a predecessor\ of\ B}OUT[P]\)
算法
输入:CFG(每个基本块的$kill_B$和$gen_B$都已算出)
输出:每个基本块的IN[B]和OUT[B]
方法:
OUT[entry] = EMPTY
for(each entry block B\entry)
OUT[B] = FULL;
while(changes to any OUT occur)
for(each basic block B\entry){
IN[B] = intersection(OUT[B.predecessors]);
OUT[B] = union(gen(B), IN[B]-kill(B));
}
对于以下例子
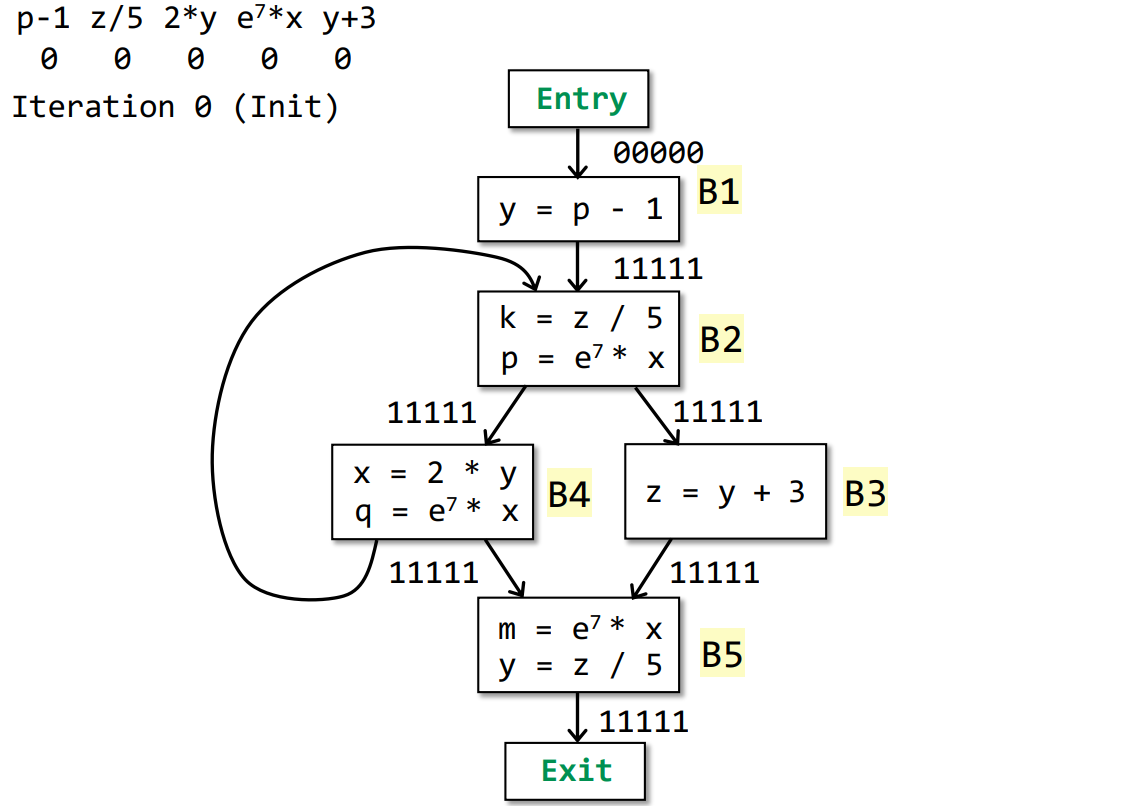
经过迭代得到
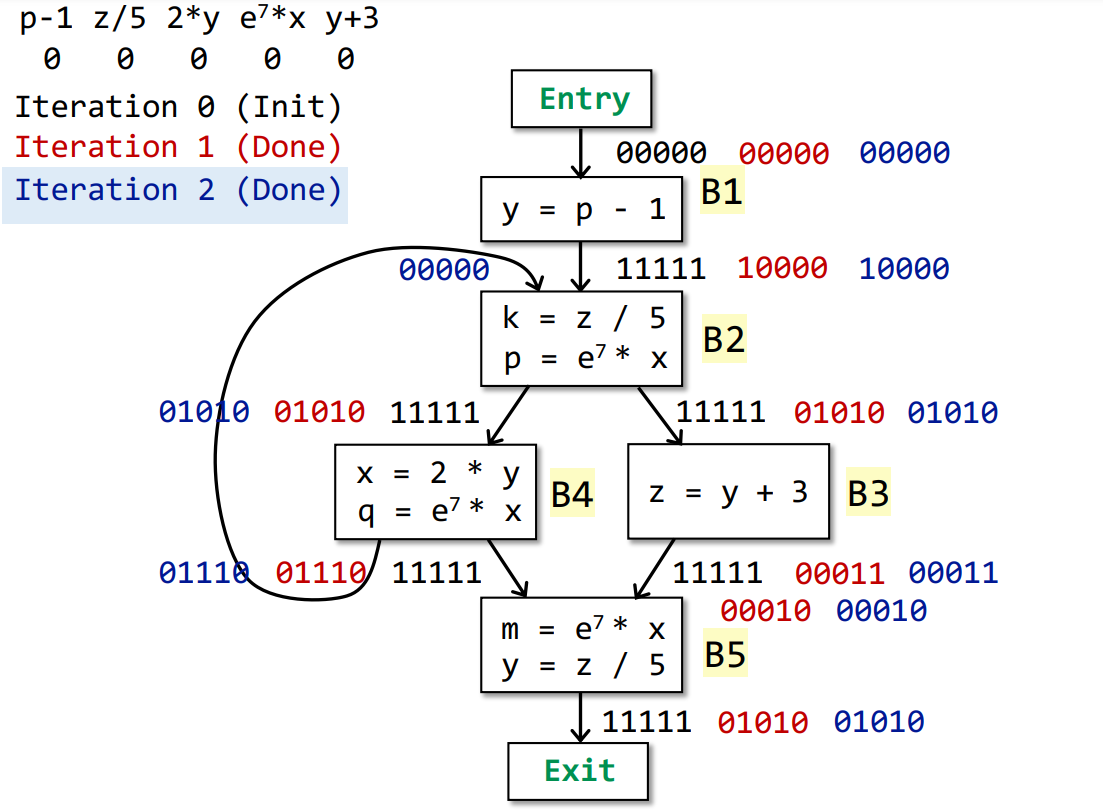
某个点的某个值为1表示这个表达式在这一点一定是可用的
对比
| Reaching Definitions | Live Variables | Available Expressions | |
|---|---|---|---|
| Domain | Definitions | Variables | Expressions |
| Direction | Forward | Backward | Forward |
| May/Must | May | May | Must |
| Boundary | OUT[entry]=empty | IN[exit]=empty | OUT[entry]=empty |
| Initialization | OUT[block]=empty | IN[block]=empty | OUT[block]=full |
| Transfer Function | gen/kill | use/def(gen/kill) | gen/kill |
| Meet | union | union | intersection |
